Kryptografia w erze transformacji cyfrowej.

Od klasycznego RSA do nowoczesnego Curve25519

Transformacja Cyfrowa (TC) to fundamentalny i ciągły proces, który wykracza poza samo wdrażanie nowych technologii. W tym dynamicznym krajobrazie fundamentem bezpieczeństwa i wydajności cyfrowego biznesu jest odpowiedni wybór algorytmów kryptograficznych. Przez lata dominował jeden z najstarszych i najbardziej rozpowszechnionych algorytmów – RSA. Dziś jednak, w obliczu rosnących wymagań dotyczących wydajności i zasobów, naturalnym następcą stała się kryptografia krzywych eliptycznych, w szczególności Curve25519. W SparkSome dostrzegamy te trendy i dlatego stale monitorujemy ewolucję zabezpieczeń, aby wspierać naszych klientów w podejmowaniu kluczowych decyzji technologicznych.

Faktoryzacja liczb pierwszych fundamentem szyfrowania RSA

Algorytm RSA, opracowany w 1977 roku, to fundament bezpieczeństwa w internecie, będący jednym z najstarszych i najszerzej stosowanych systemów szyfrowania. Jako algorytm asymetryczny, wykorzystuje parę kluczy: publiczny do szyfrowania danych i prywatny do ich odszyfrowania.

Podstawą jego bezpieczeństwa jest trudność faktoryzacji dużych liczb pierwszych.

W uproszczeniu, algorytm generuje dwie bardzo duże liczby pierwsze p i q, których iloczyn

$$n = p \cdot q$$

jest publiczny.

O ile pomnożenie tych liczb jest trywialne, o tyle rozłożenie n na pierwotne p i q jest obliczeniowo ekstremalnie trudne dla współczesnych komputerów. To sprawia, że klucz prywatny, ukryty w p i q, pozostaje bezpieczny.

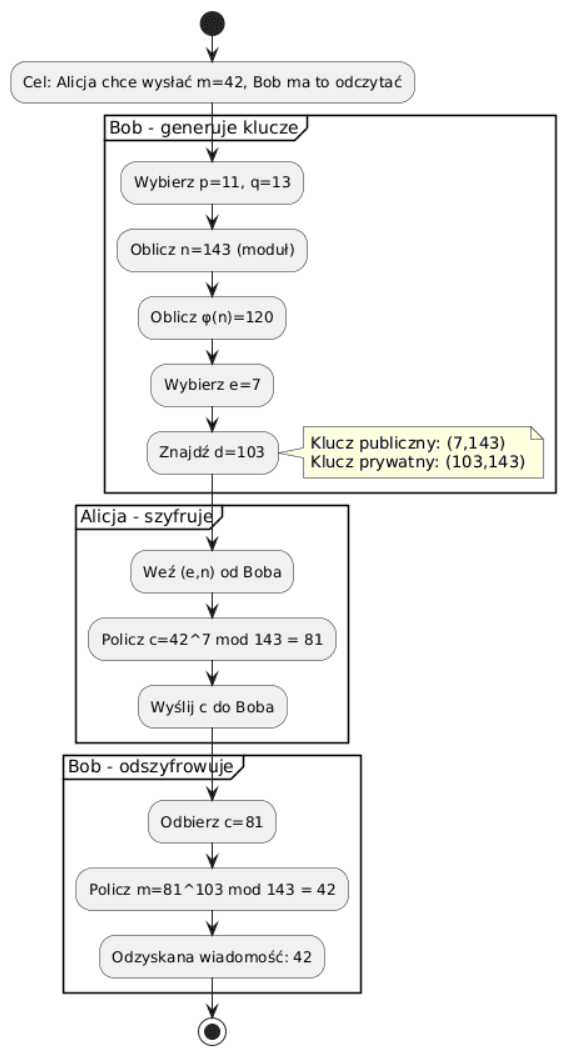
Przykład liczbowy "od A do Z" doskonale ilustruje ten mechanizm: Aby zaszyfrować wiadomość $m=42$, Generowanie par kluczy: prywatny - publiczny

Bob generuje klucze:

1. Wybiera liczby pierwsze: $p=11$, $q=13$.
2. Oblicza moduł: $n=p\cdot q=11\cdot13=143$.
3. Oblicza funkcję Eulera: $\varphi(n)=(p-1)(q-1)=10\cdot12=120$.
4. Wybiera potęgę publiczną e, która nie ma wspólnych dzielników z $\varphi(n)$, np. $e=7$.
5. Znajduje potęgę prywatną d, która jest odwrotnością modularną e modulo $\varphi(n)$, czyli liczbę spełniającą: $d \cdot e \equiv 1$ (mod 120). Używając rozszerzonego algorytmu Euklidesa, znajdujemy d:
   • $120 = 7 \cdot 17 + 1$
   • $1 = 120 - 7 \cdot 17$
   • Zatem $7 \cdot (-17) \equiv 1$ (mod 120).
   • Ponieważ $120 - 17 = 103$, to $d \equiv -17 \equiv 103$.
6. Klucz publiczny to $(e,n)=(7,143)$, a prywatny to $(d,n)=(103,143)$.

Szyfrowanie (u Alicji):

Chcemy zaszyfrować wiadomość m = 42 używając klucza publicznego dostarczonego Alicji przez Boba: $c=m^e$ mod $n=42^7$ mod 143 Używamy metody "potęgowania przez podnoszenie do kwadratu", redukując wynik modulo 143 na każdym kroku:

• $42^2 = 1764 \equiv 48$ (mod 143)
• $42^4 \equiv 48^2 = 2304 \equiv 16$ (mod 143)
• $42^7 = 42^{4+2+1} \equiv (42^4) \cdot (42^2) \cdot (42^1) \equiv 16 \cdot 48 \cdot 42$ (mod 143)
• $16 \cdot 48 = 768 \equiv 53$ (mod 143)
• $53 \cdot 42 = 2226 \equiv 81$ (mod 143)

Wynik szyfrowania to c = 81.

Deszyfrowanie (u Boba):

Bob chce odszyfrować wiadomość c = 81 używając swojego klucza prywatnego: $m=c^d$ mod $n=81^{103}$ mod 143

Rozbijamy potęgę 103 na sumę potęg dwójki: $103 = 64 + 32 + 4 + 2 + 1$. Następnie obliczamy kolejne potęgi:

• $81^2 \equiv 6561 \equiv 126$ (mod 143)
• $81^4 \equiv 126^2 \equiv 3$ (mod 143)
• $81^8 \equiv 3^2 \equiv 9$ (mod 143)
• $81^{16} \equiv 9^2 \equiv 81$ (mod 143)
• $81^{32} \equiv 81^2 \equiv 126$ (mod 143)
• $81^{64} \equiv 126^2 \equiv 3$ (mod 143)

Składamy wynik: $81^{103} \equiv (81^{64}) \cdot (81^{32}) \cdot (81^4) \cdot (81^2) \cdot (81^1) \equiv 3 \cdot 126 \cdot 3 \cdot 126 \cdot 81$ (mod 143)

• $3 \cdot 126 = 378 \equiv 92$
• $92 \cdot 3 = 276 \equiv 133$
• $133 \cdot 126 = 16758 \equiv 27$
• $27 \cdot 81 = 2187 \equiv 42$

Otrzymaliśmy z powrotem oryginalną wiadomość $m = 42$.

Mimo swojej solidności, RSA jest algorytmem zasobożernym. Operacje na dużych liczbach wymagają znacznej mocy obliczeniowej, a generowanie kluczy jest czasochłonne (ze względu na to że są to duże liczby pierwsze). Współcześnie, aby zapewnić bezpieczeństwo, wymagane są klucze o długości co najmniej 2048 lub 3072 bitów. W środowiskach o ograniczonych zasobach, takich jak urządzenia IoT, implementacja RSA bywa problematyczna.

Dlaczego Curve25519 to przyszłość bezpiecznego szyfrowania

Kryptografia krzywych eliptycznych (ECC) to podejście, które wykorzystuje zupełnie inną konstrukcję matematyczną niż RSA. Zamiast arytmetyki liczb całkowitych, opiera się na własnościach punktów na krzywej eliptycznej nad ciałem skończonym. Krzywa eliptyczna to pewna krzywa opisana równaniem, np. $y^2 = x^3 + ax + b$, która posiada strukturę grupy. Dzięki temu można dodawać do siebie punkty leżące na takiej krzywej.

Klucz prywatny to losowa liczba całkowita $n$, a klucz publiczny to punkt $Q$ na krzywej, otrzymany poprzez pomnożenie ustalonego punktu bazowego $G$ przez tę liczbę, zgodnie ze wzorem:

$$Q = n \cdot G$$

Obliczenie punktu publicznego $Q$ z klucza prywatnego $n$ jest proste. Natomiast odzyskanie $n$, znając jedynie punkty $G$ i $Q$, jest niezwykle trudnym problemem, zwanym problemem logarytmu dyskretnego na krzywej eliptycznej (ECDLP).

Kluczową zaletą kryptografii krzywych eliptycznych jest efektywność. Klucz 256-bitowy ECC zapewnia podobny poziom ochrony jak klucz RSA o długości około 3000 bitów. Mniejsze klucze to także mniej operacji na dużych liczbach, co przekłada się na większą szybkość i mniejsze zużycie mocy obliczeniowej. Ma to ogromne znaczenie dla urządzeń o ograniczonych zasobach, takich jak smartfony czy urządzenia IoT. Wśród wielu krzywych eliptycznych, szczególną popularność zdobyła Curve25519, zaprojektowana przez Daniela J. Bernsteina.

Szczegółowa analiza wymiany kluczy w mechanizmie ECDH/X25519

Aby dokładnie zrozumieć, jak to działa, przeanalizujmy uproszczony przykład, w którym dwie strony, Alicja i Bob, tworzą wspólny, tajny sekret, nie ujawniając swoich kluczy prywatnych.

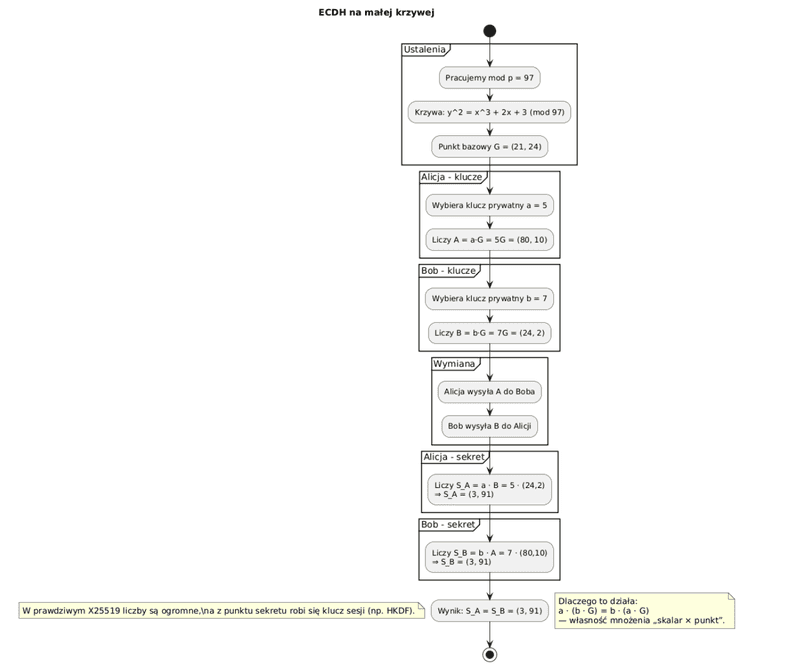
Ustalenia:

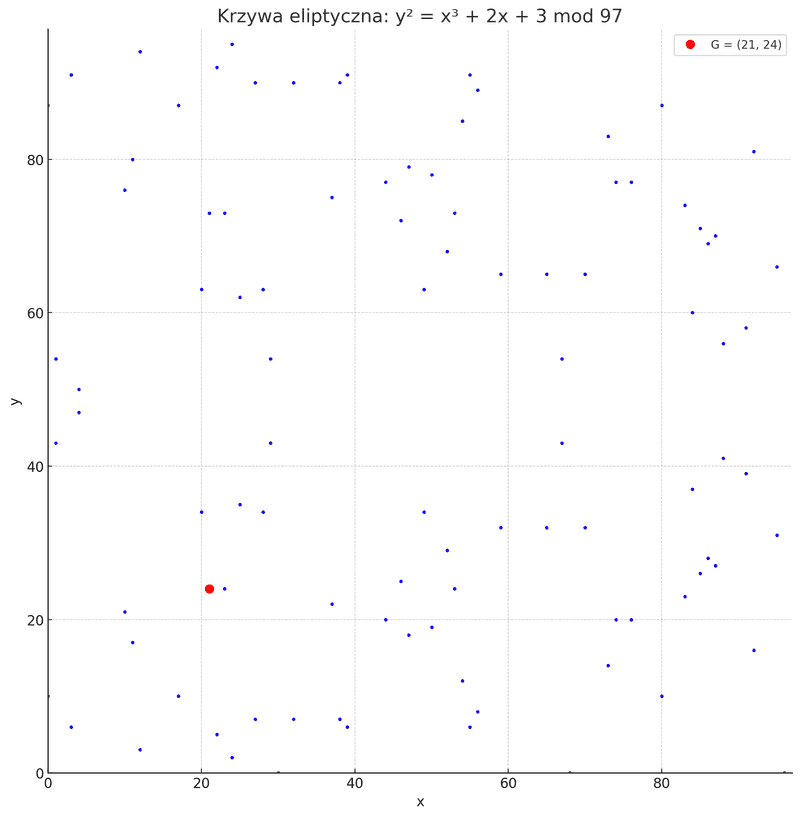
• Pracujemy modulo 97.
• Krzywa eliptyczna: $y^2 = x^3 + 2x + 3$ (mod 97).
• Punkt bazowy: $G = (21, 24)$.

Krok 1. Klucze prywatne i publiczne

• Alicja wybiera prywatnie $a = 5$, a jej klucz publiczny to $A = a \cdot G = 5G$.
• Bob wybiera prywatnie $b = 7$, a jego klucz publiczny to $B = b \cdot G = 7G$.

Krok 2. Obliczanie wspólnego sekretu Obie strony, niezależnie od siebie, obliczą ten sam punkt na krzywej, który stanie się ich wspólnym sekretem.

Alicja liczy swój sekret $S_A$: $S_A = a \cdot B = 5 \cdot (7G) = 35G$

Bob liczy swój sekret $S_B$: $S_B = b \cdot A = 7 \cdot (5G) = 35G$ Sekret jest ten sam, ponieważ mnożenie w ECC jest przemienne: $a \cdot (b \cdot G) = b \cdot (a \cdot G)$. Jest to serce algorytmu ECDH.

Krok 3. Weryfikacja na małych liczbach (przykładowe obliczenia) Obliczmy punkt $2G$, aby pokazać, jak wyglądają operacje: $2G$: $x_1 = 21, y_1 = 24$

Nachylenie stycznej $m$: $m = (3x_1^2 + 2) \cdot (2y_1)^{-1} = (3 \cdot 21^2 + 2) \cdot (2 \cdot 24)^{-1} \equiv 66$ (mod 97)

Nowa współrzędna $x$: $x_{2G} = m^2 - 2x_1 = 66^2 - 2 \cdot 21 = 4314 \equiv 46$ (mod 97)

Nowa współrzędna $y$: $y_{2G} = m(x_1 - x_{2G}) - y_1 = 66(21 - 46) - 24 = -1674 \equiv 72$ (mod 97)

Zatem, $2G = (46, 72)$.

Korzystając z tych samych zasad, można obliczyć, że zarówno $5G \cdot 7G = (3, 91)$, jak i $7G \cdot 5G = (3, 91)$. Jest to dowód na to, że obie strony dochodzą do tego samego, tajnego sekretu, bez konieczności jego wcześniejszego uzgadniania. W prawdziwym algorytmie X25519, z punktu będącego wspólnym sekretem tworzy się finalny klucz sesyjny, którym szyfrowane są dane.

Standard w nowoczesnych protokołach

Popularność Curve25519 gwałtownie wzrosła. W 2014 roku OpenSSH wprowadził mechanizm wymiany kluczy oparty na Curve25519 (tzw. ECDH Curve25519). Dziś większość nowoczesnych bibliotek kryptograficznych i protokołów posiada zaimplementowaną Curve25519. Przykładowo, protokół TLS 1.3 wymaga obsługi algorytmu X25519, a komunikatory takie jak Signal i WhatsApp wykorzystują ją do szyfrowania end-to-end. Wymianę kluczy poprzez Curve25519 wykorzystuje też nowoczesny protokół VPN WireGuard.

Ewolucja, wydajność i rola w transformacji cyfrowej

Chociaż RSA i ECC służą temu samemu celowi, ich odmienne podstawy matematyczne prowadzą do różnych implikacji technicznych i biznesowych. W nowoczesnej Transformacji Cyfrowej, gdzie kluczowe są wydajność i skalowalność, podejście oparte na ECC zyskuje przewagę. Klucze ECC są znacznie krótsze, a mimo to zapewniają porównywalny poziom bezpieczeństwa. Mniejszy klucz to mniejszy certyfikat SSL i szybszy transfer danych podczas uzgadniania połączenia. Algorytmy ECC są zazwyczaj szybsze i zużywają mniej zasobów procesora niż klasyczne RSA. Przekłada się to na niższe koszty infrastruktury, zwłaszcza w skalowalnych środowiskach chmurowych, oraz lepsze doświadczenia użytkowników.

Mimo że RSA jest historycznie dojrzałą technologią i wciąż jest powszechnie obsługiwany, nowoczesne protokoły, takie jak TLS 1.3 czy SSH, coraz częściej faworyzują krzywe eliptyczne. Curve25519 stała się de facto standardem w wielu zastosowaniach, m.in. w komunikatorach (Signal, WhatsApp) i blockchain (np. Bitcoin używa algorytmu ECDSA, opartego na krzywej secp256k1). RSA nadal odgrywa rolę jako mechanizm zapasowy lub dla kompatybilności wstecznej, ale w nowych projektach dominuje już podejście oparte na ECC, które lepiej odpowiada na potrzeby współczesnego, cyfrowego świata.

Bezpieczeństwo w świecie kwantowym – wyzwania dla działów IT

Wybór między RSA a Curve25519 nie jest już dylematem czysto technicznym, lecz strategiczną decyzją biznesową. Należy jednak pamiętać, że zarówno RSA, jak i obecnie stosowane algorytmy oparte na krzywych eliptycznych, w obliczu pojawienia się potężnych komputerów kwantowych, są teoretycznie zagrożone (algorytm Shora). Z tego powodu społeczność kryptograficzna aktywnie pracuje nad algorytmami postkwantowymi (PQC), które zastąpią obecne standardy.

W SparkSome prowadzimy bieżący monitoring tych zmian, aby nasi klienci byli gotowi na nadchodzące wyzwania. Zapewniamy, że w naszej pracy opieramy się na najnowszych i najbezpieczniejszych technologiach. W praktyce jednak, oba algorytmy – RSA i Curve25519 – przy odpowiednim doborze kluczy, są dziś uznawane za bezpieczne i stanowią solidną podstawę ochrony danych. Naszym celem jest pomoc w wyborze rozwiązania, które najlepiej odpowiada na potrzeby Twojej firmy, gwarantując zarówno wydajność, jak i najwyższy poziom bezpieczeństwa.